1954年北京坐标系、1980西安坐标系和2000国家大地坐标系是我国统一使用的坐标系统,高斯平面坐标是最为常用的坐标形式。但是在某些场景下,国家坐标系不能满足实际需求,需要建立独立坐标系进行解决。
工程测量和城市测量是需要建立独立坐标系的两个主要场景。大家知道,高斯平面坐标在投影过程中会存在投影变形。如果上世纪90年代前参加测绘工作的前辈们,对这个问题的认识会更加深刻。因为在那时GNSS还没广泛使用,控制测量主要采用经典的边角测量的方式。在进行控制网平差计算前,首先要对地面实测的边长进行改化,也就是把实测边长投影(高斯-克吕格)到参考椭球面上。改化主要包含两部分,一是把地面边长投影到椭球面上,边长会变短,称为高程归化;二是进行高斯-克吕格投影,除在中央子午线上的边长外,其他边长都会变长,距中央子午线越远,变化值越大,称为投影改化。高程归化和投影改化的具体方法可以参考《城市测量规范》2.4.12中的规定。

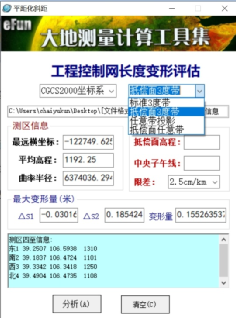
由于这两个因素,就会出现这样的情况,地面上两点的实测边长值与高斯平面坐标反算的长度值会存在差值,而且会因地点的变化而变化。这就给实际使用带来不便,比如实地测量一个地块的面积,测得各界址点的高斯平面坐标,利用界址点坐标进行面积计算,由于投影变形的影响,计算所得面积可能与地块的实际面积有很大的出入,不能满足实际需求。或者在采用高斯平面坐标的地形图上进行的设计,在图上设计的1000米的建筑,在实际建设中根据坐标放样到施工场地的长度就可能变成999.7米,这种程度的差值也是不能接受的。为了解决这个问题,在《工程测量规范》和《城市测量规范》中都要求平面坐标系统应满足投影长度变形不大于2.5cm/km。由于国家坐标系统的投影方式,只有在很少地区能够满足这个要求,可以直接使用,其余大部分地区不能满足要求,就需要建立独立坐标系统。建立独立坐标系一般有两种方式。其一是直接以一点为起点,以该点与附近另一点的方向为起始方向,建立独立坐标系。坐标系内的其他控制点以起算点和起算方向,用地面实测的边角数据进行平差计算。与国家统一坐标系的不同之处,就是地面实测的边长数据不用进行投影改化,也就是该种方法建立的独立坐标系是直接建立在地平面上的。该种方式建立的独立坐标系多在工程测量中使用,也有在一些小城镇中使用。其优点是建立过程简便,便于操作,缺点是与国家统一的坐标系缺乏联系,二者之间的转换比较困难。我在工作中曾经遇到这样一个实例,某地级市最初采用的城市坐标系,就是1992年以城市中心的一个1954年北京坐标系四等三角点为起算点,以其北另一个四等三角点(有觇标,可直接观测)的方向为起算方向,建立了独立坐标系。采用测边、测角的方式联测城市控制点,构成三角网,进行平差计算,得到控制点的平面坐标,建立城市坐标框架。为了得到该独立坐标系的与国家统一坐标系的转换参数,我们不得不把其中的部分控制点与城市周边的国家大地控制点进行联测(采用GNSS方法),得到控制点的1954年北京坐标系、1980年西安坐标系、2000国家大地坐标系的坐标。利用这些控制点的不同坐标系坐标成果,计算转换参数,确保城市独立坐标系与各国家坐标系统之间的精确转换。其二是以国家坐标系统为基础,进行投影变换,保证满足测区或城市范围内投影长度变形不大于2.5cm/km的要求,建立的独立坐标系。采用这种方法建立的坐标系,又称为抵偿坐标系。由于这种方式与国家坐标系统联系紧密,具有精确的转换关系,原有的国家坐标系统的大地控制点可以直接转换使用,在大范围的独立坐标系的建立中具有很大优势。所以,在城市独立坐标系的建立及公路、铁路等大型工程测量的独立坐标系建立中,多采用这种方式。抵偿坐标系的建立,主要有3种方法,可以根据实际情况依次采用。1、采用自定义中央子午线高斯投影平面坐标系统,其投影面采用国家坐标系参考椭球面,中央子午线的选择应考虑测区平均大地高,如果平均大地高在160m以内,中央子午线可位于测区中心,如果测区平均大地高超过160m,中央子午线可左右适当调整。2、采用具有高程抵偿面的国家统一3°带高斯平面直角坐标系统,其中央子午线与国家坐标系采用的3°带相同,投影面采用高程抵偿面,高程抵偿面一般选择为测区的平均高程面。3、采用具有高程抵偿面的自定义中央子午线高斯投影平面坐标系统,其投影面一般选择为测区的平均高程面,中央子午线位于测区中央。上面三种方法的是引用《城市坐标系统建设规范》中的专业术语来表述的,体现了专业性和严谨性。其实大家可以这样理解,以上3种方法都是在国家坐标系统的基础上,进行投影变换,以达到投影长度变形不大于2.5cm/km的目标。第1种方法只改变中央子午线,第2种方法只改变投影面,第3种方法即改变中央子午线又改变投影面。关于抵偿坐标系的建立方法已经明确,但在实际操作中可能还是有困难。首先,我们要确定一个测区的国家坐标系能否满足使用要求。需要计算测区范围内的边长投影长度变形,按照《城市测量规范》2.4.12中的公式进行计算比较繁琐,尤其是其中测距边方向参考椭球面法截弧的曲率半径Rn,需要从相关资料查取。所以,一般情况下我们都是使用大地测量计算的工具软件进行计算,省时省力,计算结果还比较可靠。在这里,我推荐一个比较好用的工具软件—大地测量计算工具集,是由军测eFun编写的一个功能丰富、实用性强的大地测量工具软件。大地测量计算工具集内有一个距离归算工具,其中的长度变形估算非常好用。把测区的东南西北四至范围各取一个点位的大地坐标(经纬度和大地高)录入到测区范围文件,导入到长度变形估算程序中,一键计算长度投影变形值。下图是计算某测区的长度变形结果,该测区的水平边长的高程归化和投影改化值刚好相抵,长度变形不大于2.5cm/km,可以直接采用国家坐标系统即可,不必建立抵偿坐标系。

当然,这样巧合的概率比较小,大部分测区还是要对国家坐标系进行投影变换,建立抵偿坐标系。建立抵偿坐标系的第一种方法比较简单,如果测区的平均大地高在160米以下,直接变换坐标系的中央子午线到测区中心即可,如果测区平均大地高超过160米,就要适当调整中央子午线,使得测区内的高程归化和投影改化的改正值正好抵消,达到测区内边长长度变形不大于2.5cm/km的目标。对于这种方法,选定了中央子午线就可以建立抵偿坐标系了,把测区内及周边的国家大地控制点的高斯平面坐标经高斯投影换带到抵偿坐标系的中央子午线,即可得到抵偿坐标系的坐标成果。建立抵偿坐标系的第二种方法就是通过调整投影面的高程以实现测区内边长长度变形不大于2.5cm/km的目标。当国家坐标系高斯平面坐标的中央子午线在测区中心时,直接调整投影面到测区平均高程面即可。当国家坐标系高斯平面坐标的中央子午线不在测区中心时,则要适当调整投影面高程以达到抵偿目标。对于这种方法,确定了投影面高程就可以建立抵偿坐标系了。在转换测区内及周边的国家大地控制点的高斯平面坐标到该抵偿系时,应首先选定一个测区中心点坐标,把各国家大地控制点与该点的距离和方位计算出来,再把距离进行投影面高程归化,利用中心点坐标、方位和高程归化后距离,计算抵偿坐标系的坐标成果。建立抵偿坐标系的第三种方法就是前两种方法的最简组合。首先把中央子午线变换到测区中心,再把投影面调整到测区平均高程面,即可建立抵偿坐标系。在转换测区内及周边的国家大地控制点的高斯平面坐标到该抵偿系时,首先高斯投影换带到抵偿坐标系的中央子午线,再按照上面第二种方法计算出国家大地控制点的抵偿坐标系成果。通过上面三种方法建立的抵偿坐标系,都可以使用大地测量计算工具集内的长度变形估算功能进行评估。分别选用任意带投影、抵偿面3度带、抵偿面任意带选项进行计算即可。
到这里,我们已经建立好了抵偿坐标系,也获得了抵偿坐标系的控制点成果。接下来,我们大概率会进行抵偿坐标系下的控制测量,在平差软件中使用该抵偿坐标系了。在我接触到的平差软件,有的能够输入投影面高程,有的不能输入投影面高程。比如我原来使用的Trimble GPS接收机的随机软件TGO,就无法输入抵偿坐标系的投影面高程,给我们抵偿坐标系下的平差计算带来困难。为解决这个问题,我参考相关专业资料,确定了可以在TGO软件中使用抵偿坐标系的两种方法。在当时还撰写了一篇论文—《TGO中抵偿坐标系的建立方法》,那大概是2010年吧,距现在很久了,原文我还保留着。为了加强大家对抵偿坐标系使用的理解,我把这篇论文附在后面。














